【实话百科】什么是CPK

前两天,之前的同时MM,微信向我求救:
登哥,什么是CPK啊?客户让我们做管控好CPK,我不知道怎么做啊。
看过这个MM的照片,你们肯定能体会到,我是无法拒绝的。

按照惯例,我们还是从5W1H的方法,来讨论这个问题。
- What,什么是CPK
- Why,为什么要用CPK
- When,什么情况下要用CPK
- Who,谁来做CPK
- Where,在哪里做CPK

什么是CPK
CPK是Complex Process Capability index的缩写,中文意思是制造过程能力指标。所以通过它的名称可以知道,CPK是一个指标,是一个衡量制造过程能力的指标。
1.1 CPK就是一个成绩
说到指标,我们可以联想到一个词叫做“成绩”,成绩也是一个指标,是用来衡量一个人或一个组织的能力的指标。
- 学生的成绩是,考试成绩越高越好
- 运动员的成绩是,百米赛跑越快越好
- 企业的成绩是,营业额越高越好
注意到没有,所有的成绩,都是越怎么样越好,这是一个单向的期望值,这个值越大(或者越小)越好。这是我们习惯的思维方式。
这个和CPK有什么关系呢?别着急,接着往下看。
我们需要仔细思考一下,在某些特性的情况下,指标不是“越怎么样越好”的。比如冰壶运动。

在冰壶运动中,不是你把冰壶扔的越远越好,也不是越近越好,而是要把冰壶刚好放在,红色中心圆的位置,这个距离越小越好。
所以从距离上来看,冰壶的目标就不是单向的越远或越近越好了,而是从近距离和远距离两个方向上,都要向中间靠近。
实际上,这也是制作行业当中,生产指标的评价方式。铅球生产厂生产的铅球,不是越重越好,而是要符合客户要求。10Kg的要求,就要努力做出10Kg的铅球,越接近越好。
1.2 CPK评价的是一个过程
我们知道了CPK是一个指标,用来评价生产的能力。但是这个指标和成绩有个一截然不同的特点,就是CPK代表着过程的能力。
运动员百米大赛,最后的成绩是一次性的,裁判不管你训练了1年还是1个星期,不管你之前跑过多么好的成绩,他只看这一次的比赛成绩。把结果拉出来一排序,谁跑的最快,谁就是冠军。
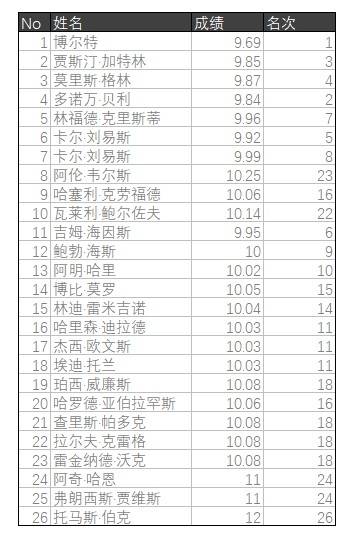
CPK的评价,不是这样的。制造生产,是一个持续的过程,不能说今天生产的产品是符合要求的,明天就不符合要求,这是不可以的。所以CPK是对一组来源与生产过程的数据进行评价。
我们可以做一个简单的测试:
- 随便拿出一张纸
- 凭着你对1cm这个长度的感觉,用这张纸,撕出10个纸条。
- 每个纸条宽度要求1cm。
- 撕完之后,找尺子把每个纸条的实际宽度量出来,记录到Excel表格中
和你的同事对比试一下,把两个人的数据放在一起,假设得到了这样的两组结果。
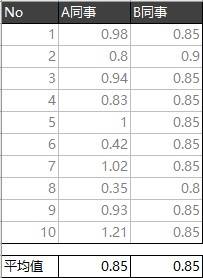
要对比这两组数据的好坏,我们很自然的就想到求平均值。
但是结果很巧,平均值是一样的,都是0.85,那么到底哪个更好一些呢?
- A同事,刚好有1次是1cm,但并不能因为这一次就说他好,因为其他的时候,都是乱七八糟的。
- B同事,基本每次都是0.85cm,非常的稳定,手非常的精准,不过就是都跑偏了。
那么要怎么评价A和B哪个更好一些呢?我们很难通过一个数值,用“越怎么样越好”的思维模式,去思考这个问题了。
这个时候就要想到CPK了,它可以很好的把这个问题,转换成了“越怎么样越好”的模式。
1.3 CPK的两个因素
前面的例子中,我们提到了AB两个同事,它们的成绩,各有各的特点。我们把这些数值,按照0.2~0.4~0.6…类似的间隔,分成几个区间,然后做一个简单的数量统计。
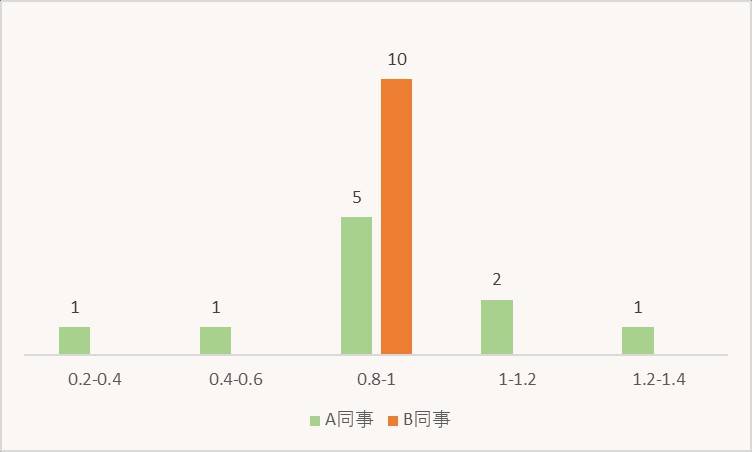
A同事生产(我们用生产来代替撕这个动作)出来的纸条宽度,比较的分散,各个区间里都有,0.8~1cm的区间里,只有5个。这种现象我常说是太粗糙,或者叫不精密,精密度差。
B同事生产出来的纸条宽度,非常的稳定。都在0.8~1cm之间,非常的精密了。但是基本都是0.85,整体跑偏了。这种现象叫做不准确,准确度差。
精密度和准确度,是CPK指标的两个因素,这两个因素通过一种计算方式结合起来,就得到了CPK的数值。所以,我们先来看一下,这两个因素,具体是什么意思。
准确度
准确度,用字母Ca来表示。表示我们实际数值的平均水平(纸条的平均宽度),与目标值(1cm)之间的差距。它是一个百分比值,这个值越小,表示离目标值越接近,评价结果越好。计算公式是这样的。
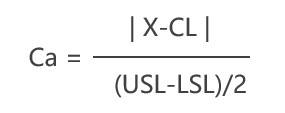
精确度
精确度,用字母Cp来表示。表示实际数值的分布状况。精确度越大,表示实际数值越集中,评价结果越好。精确度与目标值关系不大。
那么要怎么表现数值的分布状况呢?这里要用到一个专业的计算方法,叫做标准偏差σ,或者叫sigma。
这个函数我们在上学的时候,学习统计课的时候,学习过。相信大部分人都已经还给老师了。
然后我们需要根据sigma来计算出Cp。计算公式是这样的。
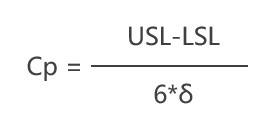
有了准确度Ca和精确度Cp之后,我们可以通过下面的公式,计算出CPK来。
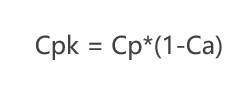
现在看不懂公式,没有关系,接下来我会详细的解释。
1.4 CPK的计算公式
下面即将进入一段高能烧脑的学术描述,请仔细研读下面的用户说明,如不同意,请关闭此页面。
- 不要问我,为什么CPK的公式是Cp*(1-Ca),而不是Ca*(1-Cp),我也不知道
- 我只是描述公式的计算过程,具体含义不要问我。
- 不要盲目的点赞,请转发完之后,再点赞。
我同意以上协议
CPK的计算公式非常的简单,我们优先说明一下准确度和精确度的公式。

准确度Ca
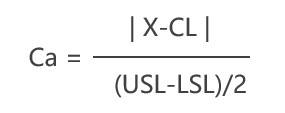
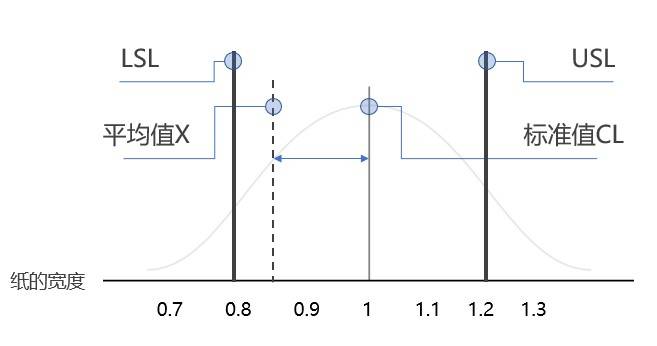
从准确度的计算公式中,我们可以看到,公式的实际意义,就是把实际数值的平均值,和目标值的差距(比如我们叫做D),和要求的标准偏移范围(USL-LSL)/2的比值。
USL和LSL是客户给出的数值的上下限。还是用撕纸条来举例子,说明一下USL和LSL的意义。
虽然目标是1cm宽的纸条,但我知道你肯定不会那么准确的,撕出宽度刚好是1cm的纸条,所以给你一范围,纸条的宽度要在0.8 ~1.2cm之间,这样才更好达到目标。
这个0.8LSL就是LSL,1.2cm就是USL。
别问我UCL和LCL是什么,这又是另外一个话题。
USL-LSL是固定不变的,目标值CL也是不变的,所以:
- 实际数值的平均值,越远离CL,Ca越大,CPK越差。
- 实际数值的平均值,越接近CL,Ca越小,CPK越好。
精确度Cp

从精确度Cp的公式中,我们可以看到,用上下限之间的宽度(USL-LSL),除以6*sigma,就是精确度。
USL-LSL是固定不变的,而sigma是分母,又表示的是数值的分散程度。所以:
- 实际数值越分散,sigma越大,Cp越小,CPK越差。
- 实际数值越集中,sigma月小,Cp越大,CPK越好。
不要问我为什么乘以6,这是六西格玛的问题,又是非常大的话题。
CPK
明白了Ca和Cp的公式,CPK的计算就非常的简单了。一个小学生都会的计算。
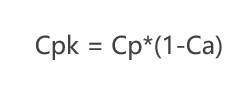
通过对于Ca和Cp的分析,我们可以知道,CPK也是越大越好的。
不要问我,为什么CPK一定要大于1.33,质量专家要求的,我也不知道。
1.5 在Excel中计算CPK
明白了CPK的含义,以及公式之后,我们就可以在Excel中,对A和B两个同事的撕纸条比赛,进行一个评比了。
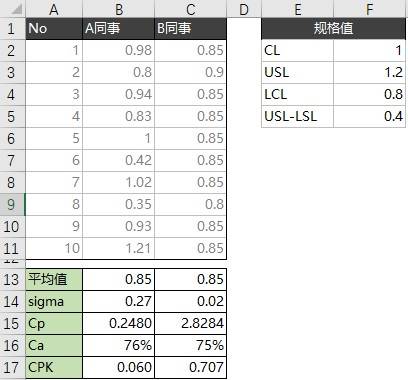
通过对比CPK,我们认为B同事要比A同事好,虽然他的CPK也没有达到1.33。
我简单的说明一下,每个参数,使用到的Excel公式。
- 平均值,使用average函数
- sigma,使用STDEV()函数,2016版Excel,使用STDEV.P()函数。
- 其他函数,使用都是简单的加减乘除。
具体的算法,我就不讲解了下载Excel案例表格,可以直接查看公式。
关注品管大实话,回复CPK,获取下载链接。

为什么要用CPK
通过前面的长篇大论,终于明白了什么是CPK,那为什么一定要用CPK,就比较清晰了。
使用简单的“越怎么样越好”的思维模式,很难评价这一组数据,哪个好,哪个不好,平均值都一样的嘛。所以要用另外一种方式,把这一组过程数据,转换成“越怎么样越好”的思维模式,这个方式就是CPK。

什么情况下用CPK
当统计的数据,不是一个单向的期望值,不能用越怎么样越好来表述的时候,可以考虑用CPK来体现。

谁来做CPK
CPK是一个常用的计算方法,一个知识技能,谁都可以学,谁都可以用。

在哪里用CPK
实话实说,应付客户的时候,要用CPK。回答完毕。
起立!下课!
如果你喜欢我的文章,欢迎打赏支持。

本文完
源自拉登Dony的公众号【品管大实话】
转载请注明出处
联系作者
这是我见过的最通俗易懂的CPK教程,拉登老师超级棒
感谢认可,太懒了,后面还要继续加油写
看了妹子的照片,我相信你是没法拒绝的
好文章!666,学习了